Research
I currently do research in convex optimization, with a focus on semidefinite relaxations, polynomial and sum of squares optimization, and solving large-scale problems.
Global Landscape of Low-Rank Sum of Squares
Semidefinite programming is powerful but slow, can we speed it up by using first order methods? By factorizing the PSD variable \(X = UU^\top\), we can optimize over \(U\) using first-order methods. However this formulation is nonconvex and these methods may get stuck in local minima. We show that this does not happen in the setting of univariate sum of squares decomposition: all local minima are global. In addition, using an interpolation representation we can compute gradients in near-linear time (using TrigPolys.jl), finding the sum of squares decomposition of a million-degree polynomial in less than 30 minutes.
Benoît Legat*, Chenyang Yuan* and Pablo Parrilo. “Low-Rank Univariate Sum of Squares Has No Spurious Local Minima” Preprint. [arxiv]
Talks:
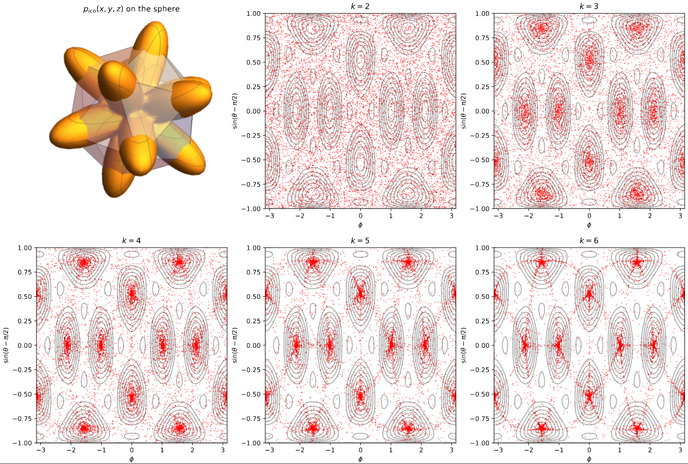
Rounding Convex Relaxations of Quadratic Maps
This line of work studies convex relaxations of functions of the form \(f(x^T A_1 x, \ldots, x^T A_d x)\). For very high degree but structured polynomials we derive intermediate relaxations interpolating between spectral and Sum-of-Squares relaxations, as well as randomized rounding schemes (see picture on the right). We also analyze rounding schemes for different functions \(f\), making a connection to Max-Cut.
Chenyang Yuan and Pablo Parrilo. “Semidefinite Relaxations of Products of Nonnegative Forms on the Sphere” Preprint. [arxiv]
Talks:
Permanent Approximation
We found a connection between approximating the permanent of a PSD matrix and approximating the maximum of a polynomial optimization problem on the sphere. By doing so our analysis improve the approximation factor, in addition to simplifying its proof.
Chenyang Yuan and Pablo Parrilo. “Maximizing Products of Linear Forms, and The Permanent of Positive Semidefinite Matrices”, Mathematical Programming Series A, 2021. [link] [arxiv] [pdf]
Talks:
- MIT CS Theory Lunch 2020 [notes]
Focused Polynomials
Masters thesis work on characterizing classes of polynomial optimization problems on the sphere that can be compressed by a random projection. Introduced the notion of polynomials generated from focused cones, and the reduced dimension depends on the Gaussian width of the focused cones.
Chenyang Yuan. “Focused Polynomials, Random Projections and Approximation Algorithms for Polynomial Optimization over the Sphere” S.M. thesis, MIT. [pdf] [dspace]
Class Projects
Hardness Results for the Discrete Gauss Transform (DGT)
Class project for 6.850 (Geometric Computing) together with with Kyriakos Axiotis and Aleksandar Makelov. We prove a new hardness result for the DGT (used in physical simulations, evaluating and optimizing over Gaussian kernels) assuming the Strong Exponential Time Hypothesis. [pdf]
Control of Queueing Networks
Undergrad research in Alex Bayen’s group at UC Berkeley studying the effect of attacks on mobility as a service networks (such as Uber or Lyft) by an adversary gaining control of a fraction of the network, and how we can deter these attacks. We model this problem as a queueing network and the attacker or operator aims to optimally control a fraction of the agents in the network to meet some objective.
J. Thai, C. Yuan, A. Bayen. “Resiliency of Mobility-as-a-Service Systems to Denial-of-Service Attacks”, IEEE Transactions on Control of Network Systems. [link] [pdf]
C. Yuan, J. Thai, A. Bayen. “ZUbers against ZLyfts Apocalypse: An Analysis Framework for DoS Attacks on Mobility-as-a-Service Systems”, ACM/IEEE International Conference on Cyber-Physical Systems. [link] [pdf]